Understanding Radiance (Brightness), Irradiance and Radiant Flux
Author: H. Zhu and P. Blackborow
Introduction
Evaluation of the performance of a radiation source has to involve radiometry – the measurement of quantities associated with radiation. To those new to the field, the units and terms, such as Radiance, Irradiance and Radiant Flux, may be unfamiliar. In addition, non-standard terms such as brightness, radiant power, flux, and intensity are often used casually without explanations. Finally, photometry terms such as luminance are often misused when discussing radiometry situations.
This Application Note attempts to explain radiometry terms and units, to differentiate them from photometry terms, and to clarify the non-standard terms commonly heard. In addition, we will illustrate how the radiometric terms help in selecting an appropriate light source for a particular application.
Definitions of Radiometry and Photometry
Radiometry is the science of measuring radiation energy in any portion of the electromagnetic spectrum. In practice, the term is usually limited to the measurement of ultraviolet (UV), visible (VIS), and infrared (IR) radiation using optical instruments.
Photometry is the science of measuring visible radiation, light, in units that are weighted according to the sensitivity of the human eye. It is a quantitative science based on a statistical model of the human visual perception of light (eye sensitivity curve) under carefully controlled conditions.
Broadband radiation sources emitting UV-VIS-IR wavelength radiation, such as Energetiq’s Laser-Driven Light Sources (LDLS™), are characterized using radiometry and its units. On the other hand, industrial lighting and household lighting products (lamps) and illumination designs are characterized using photometry and its units.
Definition of the frequently used Radiometry Units
The SI System (Système International d’unités) defines six radiometric units, of which three are most commonly used for describing the effectiveness of radiation coupling between a light source and an optical system. These most commonly used units are: (1) Radiance; (2) Irradiance; and (3) Radiant Flux. Radiance is often casually called “brightness”, a term also used in photometry to describe the perception of human eyes looking at a light source. An example of brightness perception will be given in the following section.
Radiance
The SI unit of radiance is watts per square meter per steradian [W/m2-sr]. Since many radiation sources used in laboratories have emitting area in the square millimeters range, the unit of milliwatts per square millimeter per steradian [mW/mm2-sr] is often used for radiance. As shown in Figure 1, the radiance (R) of the source emitting area (A) equals the radiation power (P), which is emitted from A and propagates in solid angle Ω, divided by the area A and the solid angle Ω: R = P / (A x Ω).
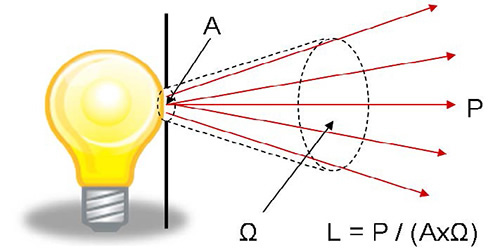
Figure 1. (left) Radiance (R) of source is the Power (P) emitted from the source emitting Area (A) and propagated in the Solid Angle (Ω).
The steradian [sr] is the SI unit for measuring solid angles, defined by the solid angle (Ω) that projects on the surface of a sphere with a radius of r, having an area (A) equal to r2 (Ω = A/r2 = r2/r2 = 1 [sr]). It describes angular spans in three-dimensional space, analogous to the way in which the radian [rad] describes angles in a two-dimensional plane. The total solid angle for a point in space is 4π steradians.
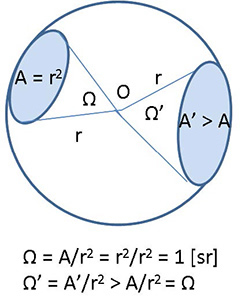
Figure 2. (left) Steradian [sr] is a unit for measuring solid angles (Ω) defined by the solid angle that projects on the surface of a sphere, with a radius of r, having an area of A = r2 (Ω = A/r2 = r2/r2 = 1 [sr]).
The radiance of a source is increased by increasing its emitted power, by making the emitting area of the source smaller or by emitting the radiation into a smaller solid angle. Strictly speaking, radiance is defined at every point on the emitting surface, as a function of position, and as a function of the angle of observation. Often, as in the example above we use radiance of a source to mean the radiance averaged over a finite sized aperture and over some solid angle of interest.
Radiance is a conserved quantity in an optical system so that radiance measured as watts per unit area per unit solid angle incident on a detector will not exceed the radiance at the emitter. In practice, for any bundle of rays mapping an emitter to a detector, the radiance seen at the detector will be diminished by the light which is absorbed along the way or scattered out of the solid angle of the bundle of rays reaching the detector.
Let us consider an example. Suppose one observes with the eye a 35W Xenon (Xe) short-arc lamp, and then a 60W straight tube fluorescent lamp, both at a similar distance of a few meters. (As background information, the 35W arc lamp emits significantly less visible power than the 60W fluorescent tube.) Which light source is perceived to be brighter, or in radiometric terms, has higher radiance? The Xe short-arc lamp is perceived to be much brighter, although the 35W arc lamp emits less power than the 60W fluorescent lamp. This is as a result of the much smaller emitting area (A) of the short-arc lamp compared to the very large emitting area of the fluorescent lamp, while the eye is receiving the radiation at more or less the same solid angle (Ω) when the distance between the eye and the source is the same. The eye’s lens forms a bright image of the Xe arc on a very small area of the retina and the eye does not feel comfortable. The larger area fluorescent lamp will form an image over a much larger area on the retina, which the eye can tolerate more comfortably. The arc-lamp has a much higher radiance than the fluorescent lamp, even though it emits less power.
By way of a further example, imagine using the Xe and fluorescent lamps to illuminate a small area such as the end of a 200 μm diameter optical fiber. As a result of the higher source radiance the radiation from the 35W Xe arc-lamp can be much more efficiently collected and focused into the fiber. In contrast, the low radiance 60W fluorescent lamp will be ineffective in coupling its radiation energy into the fiber, no matter what type of focusing optic is used.
Energetiq’s Laser-Driven Light Sources have ultrahigh radiance from their small emitting area (~ 100 μm diameter). Radiation from such a high radiance and small emitting area source can be even more efficiently coupled into the 200 μm diameter optical fiber described above. This is also true for other optical systems with small apertures and a limited accepting solid angle - optical systems with small ‘étendue’ - such as the narrow slits of a monochromator. (For further discussion of étendue, see Application Note #002-2-14-2011, Etendue and Optical Throughput Calculations.)
Irradiance
Irradiance is the radiometry term for the power per unit area of electromagnetic radiation incident on a surface. The SI unit for irradiance is watts per square meter [W/m2], or milliwatts per square millimeter [mW/mm2]. (Irradiance is sometimes called intensity, but this usage leads to confusion with another standard, but infrequently used, radiometry unit —Radiant Intensity — which is measured in watts per steradian.)
If a point radiation source emits radiation uniformly in all directions and there is no absorption, then the irradiance drops off in proportion to the distance squared from the source, since the total power is constant and it is spread over an area that increases with the distance squared from the radiation source. To compare the irradiance of different sources, one must take into account the distance from the source. A 50 cm distance is often used for such measurements.
Irradiance is a useful measure for applications where power must be delivered to large areas. For example, illuminating a classroom or a football field is primarily a question of delivering a certain number of watts per square meter. This can be achieved by using a single high power source. However, since irradiance does not depend on solid angle, multiple sources can be combined, illuminating the walls or the field from different angles.
The irradiance of a source is not the most useful measure when designing an efficient optical coupling system that collects radiation from a source, and then delivers the radiation into an optical instrument. Such optical instruments will have a limited entrance aperture and a limited acceptance solid angle. In such cases it is the radiance of the source (its ‘brightness’) that is most useful.
Radiant Flux
Radiant flux is radiant energy per unit time, also called radiant power [W, mW or μW]. Radiant flux is often used to describe the radiation power output of a radiation source, or the radiation power received by an optical instrument. Examples of radiant flux are: the radiation power passing through a pinhole; the radiation power emerging from the optical fiber of a fiber-coupled laser; the radiation power received by a power detector.
The units of Radiant Flux do not include area or solid angle, and are therefore not helpful in determining whether a particular light source with a particular radiant flux will be useful in delivering its power to an optical instrument. In our earlier example, the 60W fluorescent tube emits a greater radiant flux (power) than the 35W Xe arc-lamp. But, with an appropriate focusing optic, the arc lamp will deliver a higher radiant flux to the 200μm diameter optical fiber. A Laser-Driven Light Source, such as Energetiq’s EQ-99, may have a lower radiant flux emitted than the 35W arc-lamp, but its higher radiance allows it to deliver even higher radiant flux to the 200 μm diameter optical fiber than the 35W arc-lamp.
Spectral Radiance, Spectral Irradiance, and Spectral Radiant Flux
The three terms discussed above are quantities used to characterize radiation within a certain wavelength band, (UV, VIS and/or IR). It is also common to consider those values for unit wavelength (per nm) in the spectrum. For radiation power per unit of wavelength, spectral radiant flux is used with SI units of watts per meter [W/m], or more commonly milliwatts per nanometer [mW/nm]. For radiation incident on a surface, the term spectral irradiance is used, and has the SI unit of [W/m3], or more commonly units of [mW/mm2-nm]. For radiation power within a unit solid angle from a unit emitting area and unit wavelength, the term is spectral radiance, most commonly with units of [mW/mm2-nm-sr].
Spectral radiance is a key measure when selecting a source for an application. In general, most radiation sources exhibit variations in spectral radiance across their spectrum of emission. In Figure 3, the spectral radiance is shown for a 30W deuterium lamp (D2), a 75W high-brightness Xe arc-lamp, and for two versions of Energetiq’s Laser-Driven Light Source, the EQ-99 and the EQ-1500.
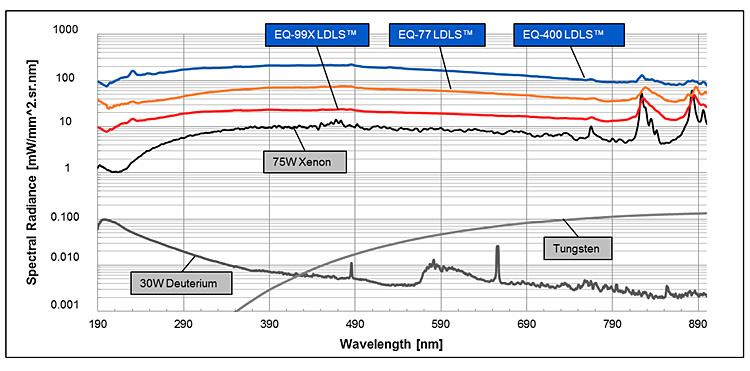
Figure 3: Spectral radiance of EQ-99X LDLS, EQ-77 LDLS, EQ-400, LDLS, 75W short-arc Xe Lamp, Tungsten Lamp and D2 lamp.
For our earlier example of illuminating a 200 μm optical fiber, let us assume that we wish to compare the four light sources in Figure 3 at delivering 200 nm wavelength radiation into the fiber. Since the key parameter is the spectral radiance of the sources at 200 nm, we can see from Figure 3 that the Xe lamp’s spectral radiance is about one order of magnitude higher (‘brighter’) than the D2 lamp and the LDLS sources are a further order of magnitude higher than the Xe lamp. With the same focusing optic used to couple the light from each source into the 200 μm fiber, the radiant flux delivered into the fiber would similarly vary by the same orders of magnitude.
Conclusions
In the design of optical instruments, scientists and engineers choosing light sources will be exposed to a variety of source specifications and radiometric terms. It is important to understand the nature of the specifications and to couch them in radiometric terms that will enable appropriate design decisions. In general, for typical optical instrument applications, such as spectroscopy and imaging, it is the radiance and spectral radiance of the light source that most needs to be understood. For an instrument with limiting apertures and solid angles, it is the radiance of the source that determines how much radiation passes through the instrument. By carefully matching the instrument with a source of appropriate radiance, an optimum system can be designed.


![Download Technical Note [PDF]](https://no-cache.hubspot.com/cta/default/5512327/c433a211-ccd8-41d8-8760-b957ac6e69e9.png)